سوال

سوال : در شکل زیر، نقطه های B و C بر پاره خط AD واقعند و AB ، BC ، CD به ترتیب قطرهای دوایر به مراکز O ، N ، P هستند. شعاع هر یک از این دوایر برابر ۱۵ است و پاره خط AG بر دایره ی P مماس است و دایره ی N را در E و F قطع می کند. طول وتر EF چند است؟

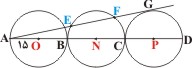
پاسخ : با توجه به این که شعاع دایره در نقطه ی تماس بر خط مماس عمود است زاویه ی PGA قائمه است. پاره خط NH را بر AG عمود رسم می کنیم.

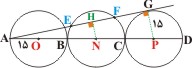
در مثلث APG می توان رابطه ی تالس را نوشت :

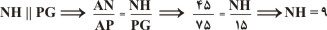
با توجه به رابطه ی فیثاغورس در مثلث قائم الزاویه ی NFH خواهیم داشت :

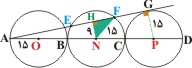
۱۴۴ = ۸۱ - ۲۲۵ = ۹^۲ - ۱۵^۲ = HF^۲=   NF^۲ - NH^۲

۱۲ = HF

EF دو برابر HF است. بنابراین ۲۴ = EF