اشکال هندسی
کره و استوانه
علاوه بر مطالب فوق هندسه فضایی به مطالعه کره و استوانه نیز میپردازد. معادله متعارف کره به شعاع a و مرکز به صورت زیر است:
به صورت زیر است:

در مورد استوانه و مطالعه درباره استوانه ناچار به تعمیم هندسه تحلیلی به فضا هستیم. به طور کلی استوانه سطحی است که از حرکت خط مستقیم در امتداد یک منحنی تولید میشود به طوری که همواره موازی خط میباشد. به طور کلی ، هر منحنی مانند در صفحه
در صفحه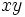 استوانهای در فضا تعریف میکند که معادله آن به صورت فوق میباشد و از نقاط خطوطی مار بر منحنی تشکیل شده است که با محور z موازیاند. خطوط را گاهی عناصر استوانه مینامند. بحث فوق را میتوان برای استوانههایی که عناصرشان موازی سایر محورهای مختصاتاند تکرار کرد. به طور خلاصه: یک معادله در مختصات دکارتی ، که از آن یکی از مختصات متغیر حذف شده، نمایش استوانه ای است که عناصرش موازی محور مربوط به متغیر مفقود است. سهمی گونها یکی دیگر از اشکال مختصات فضایی هستند. بسیاری از آنتنها به شکل قطعاتی از سهمی گونهای دوارند، رادیو تلسکوپها یکی دیگر از انواع سهمی گونهای مورد استفاده بشر هستند که در ساخت آنها از هندسه فضایی مدد گرفته شده است.
استوانهای در فضا تعریف میکند که معادله آن به صورت فوق میباشد و از نقاط خطوطی مار بر منحنی تشکیل شده است که با محور z موازیاند. خطوط را گاهی عناصر استوانه مینامند. بحث فوق را میتوان برای استوانههایی که عناصرشان موازی سایر محورهای مختصاتاند تکرار کرد. به طور خلاصه: یک معادله در مختصات دکارتی ، که از آن یکی از مختصات متغیر حذف شده، نمایش استوانه ای است که عناصرش موازی محور مربوط به متغیر مفقود است. سهمی گونها یکی دیگر از اشکال مختصات فضایی هستند. بسیاری از آنتنها به شکل قطعاتی از سهمی گونهای دوارند، رادیو تلسکوپها یکی دیگر از انواع سهمی گونهای مورد استفاده بشر هستند که در ساخت آنها از هندسه فضایی مدد گرفته شده است.
منشور
منشور قائم شکلی فضایی است که از دو یا چند ضلعی مساوی و موازی تشکیل شده که رئوس این چندضلعیها طوری به هم وصل شده اند که وجوه جانبی این شکل فضایی مستطیل میباشد.
مکعب مستطیل
مکعب مستطیل منشوری است که قاعدههای آن مستطیل میباشد اگر ابعاد قاعده مکعب مستطیل b , a و ارتفاع آن c باشد خواهیم داشت:
هرم
هرم شکلی است فضایی که قاعده آن یک یا چند ضلعی است و وجوه جانبی آن مثلث است. این مثلثها یک رأس مشترک به نام S دارند. هرمی که قاعده آن مربع باشد هرم مربع القاعده و هرمی که قاعده آن مثلث باشد هرم مثلث القاعده نامیده میشود. پاره خطی که از رأس هرم بر صفحه قاعده آن عمود میشود ارتفاع نامیده میشود. اگر قاعده یک هرم یک چند ضلعی منتظم باشد پای ارتفاع آن بر مرکز قاعده منطبق باشد، هرم را هرم منتظم مینامیم. ارتفاع هر وجه جانبی هرم منتظم را سهم هرم مینامند.
مخروط
اگر یک مثلث قائم الزاویه را حول یکی از اضلاع زاویه قائمه دوران دهیم شکلی فضایی پدید میآید که مخروط نامیده میشود. در این صورت ضلعی که مثلث را حول آن دوران دادهایم ارتفاع مخروط و ضلع دیگر زاویه قائمه شعاع قاعده مخروط و وتر مثلث مولد مخروط میباشد.
علاوه بر مطالب فوق هندسه فضایی به مطالعه کره و استوانه نیز میپردازد. معادله متعارف کره به شعاع a و مرکز
 به صورت زیر است:
به صورت زیر است:
در مورد استوانه و مطالعه درباره استوانه ناچار به تعمیم هندسه تحلیلی به فضا هستیم. به طور کلی استوانه سطحی است که از حرکت خط مستقیم در امتداد یک منحنی تولید میشود به طوری که همواره موازی خط میباشد. به طور کلی ، هر منحنی مانند
 در صفحه
در صفحه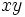 استوانهای در فضا تعریف میکند که معادله آن به صورت فوق میباشد و از نقاط خطوطی مار بر منحنی تشکیل شده است که با محور z موازیاند. خطوط را گاهی عناصر استوانه مینامند. بحث فوق را میتوان برای استوانههایی که عناصرشان موازی سایر محورهای مختصاتاند تکرار کرد. به طور خلاصه: یک معادله در مختصات دکارتی ، که از آن یکی از مختصات متغیر حذف شده، نمایش استوانه ای است که عناصرش موازی محور مربوط به متغیر مفقود است. سهمی گونها یکی دیگر از اشکال مختصات فضایی هستند. بسیاری از آنتنها به شکل قطعاتی از سهمی گونهای دوارند، رادیو تلسکوپها یکی دیگر از انواع سهمی گونهای مورد استفاده بشر هستند که در ساخت آنها از هندسه فضایی مدد گرفته شده است.
استوانهای در فضا تعریف میکند که معادله آن به صورت فوق میباشد و از نقاط خطوطی مار بر منحنی تشکیل شده است که با محور z موازیاند. خطوط را گاهی عناصر استوانه مینامند. بحث فوق را میتوان برای استوانههایی که عناصرشان موازی سایر محورهای مختصاتاند تکرار کرد. به طور خلاصه: یک معادله در مختصات دکارتی ، که از آن یکی از مختصات متغیر حذف شده، نمایش استوانه ای است که عناصرش موازی محور مربوط به متغیر مفقود است. سهمی گونها یکی دیگر از اشکال مختصات فضایی هستند. بسیاری از آنتنها به شکل قطعاتی از سهمی گونهای دوارند، رادیو تلسکوپها یکی دیگر از انواع سهمی گونهای مورد استفاده بشر هستند که در ساخت آنها از هندسه فضایی مدد گرفته شده است.منشور
منشور قائم شکلی فضایی است که از دو یا چند ضلعی مساوی و موازی تشکیل شده که رئوس این چندضلعیها طوری به هم وصل شده اند که وجوه جانبی این شکل فضایی مستطیل میباشد.
مکعب مستطیل
مکعب مستطیل منشوری است که قاعدههای آن مستطیل میباشد اگر ابعاد قاعده مکعب مستطیل b , a و ارتفاع آن c باشد خواهیم داشت:
a+b)2c) = مساحت جانبی مکعب مستطیل
(ab+ac+bc)2=2ab+(2bc+2ac)= مساحت کل مکعب مستطیل
Abc= حجم مکعب مستطیل
(ab+ac+bc)2=2ab+(2bc+2ac)= مساحت کل مکعب مستطیل
Abc= حجم مکعب مستطیل
هرم
هرم شکلی است فضایی که قاعده آن یک یا چند ضلعی است و وجوه جانبی آن مثلث است. این مثلثها یک رأس مشترک به نام S دارند. هرمی که قاعده آن مربع باشد هرم مربع القاعده و هرمی که قاعده آن مثلث باشد هرم مثلث القاعده نامیده میشود. پاره خطی که از رأس هرم بر صفحه قاعده آن عمود میشود ارتفاع نامیده میشود. اگر قاعده یک هرم یک چند ضلعی منتظم باشد پای ارتفاع آن بر مرکز قاعده منطبق باشد، هرم را هرم منتظم مینامیم. ارتفاع هر وجه جانبی هرم منتظم را سهم هرم مینامند.
2/سهم×محیط قاعده= مساحت جانبی هرم منتظم
ارتفاع×مساحت قاعده ×1/3 = حجم هرم
ارتفاع×مساحت قاعده ×1/3 = حجم هرم
مخروط
اگر یک مثلث قائم الزاویه را حول یکی از اضلاع زاویه قائمه دوران دهیم شکلی فضایی پدید میآید که مخروط نامیده میشود. در این صورت ضلعی که مثلث را حول آن دوران دادهایم ارتفاع مخروط و ضلع دیگر زاویه قائمه شعاع قاعده مخروط و وتر مثلث مولد مخروط میباشد.
2 / مولد مخروط×محیط قاعده مخروط = مساحت جانبی مخروط
ارتفاع×مساحت قاعده×1/3 = حجم مخروط
ارتفاع×مساحت قاعده×1/3 = حجم مخروط
+ نوشته شده در دوشنبه بیست و چهارم آبان ۱۳۸۹ ساعت توسط بهزادی
|
 این وبلاگ برای برقراری ارتباط با همه ی علاقمندان ریاضی ساخته شده است، لیسانس ریاضی خودمو از دانشگاه فرهنگیان اهواز گرفتم و در حال حاضر دانشجوی ارشد ریاضی روزانه گرایش انالیز از دانشگاه شهرکرد هستم، ایمیل من
این وبلاگ برای برقراری ارتباط با همه ی علاقمندان ریاضی ساخته شده است، لیسانس ریاضی خودمو از دانشگاه فرهنگیان اهواز گرفتم و در حال حاضر دانشجوی ارشد ریاضی روزانه گرایش انالیز از دانشگاه شهرکرد هستم، ایمیل من